Page 47 - Mathematics Class - XII
P. 47
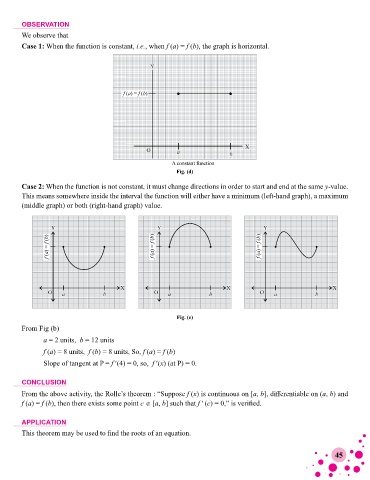
OBSERVATION
We observe that
Case 1: When the function is constant, i.e., when f (a) = f (b), the graph is horizontal.
Fig. (d)
Case 2: When the function is not constant, it must change directions in order to start and end at the same y-value.
This means somewhere inside the interval the function will either have a minimum (left-hand graph), a maximum
(middle graph) or both (right-hand graph) value.
Fig. (e)
From Fig (b)
a = 2 units, b = 12 units
f (a) = 8 units, f (b) = 8 units, So, f (a) = f (b)
Slope of tangent at P = f ′(4) = 0, so, f ′(x) (at P) = 0.
CONCLUSION
From the above activity, the Rolle’s theorem : “Suppose f (x) is continuous on [a, b], differentiable on (a, b) and
f (a) = f (b), then there exists some point c ∈ [a, b] such that f ' (c) = 0,” is verified.
APPLICATION
This theorem may be used to find the roots of an equation.
45