Page 46 - Mathematics Class - XII

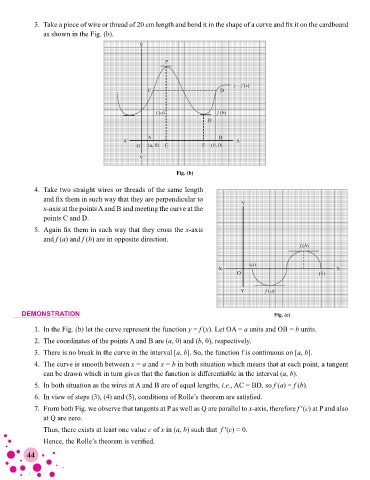
3. Take a piece of wire or thread of 20 cm length and bend it in the shape of a curve and fix it on the cardboard
as shown in the Fig. (b).

Fig. (b)

4. Take two straight wires or threads of the same length
and fix them in such way that they are perpendicular to
x-axis at the points A and B and meeting the curve at the
points C and D.
5. Again fix them in such way that they cross the x-axis
and f (a) and f (b) are in opposite direction.

DEMONSTRATION Fig. (c)

1. In the Fig. (b) let the curve represent the function y = f (x). Let OA = a units and OB = b units.
2. The coordinates of the points A and B are (a, 0) and (b, 0), respectively.

3. There is no break in the curve in the interval [a, b]. So, the function f is continuous on [a, b].
4. The curve is smooth between x = a and x = b in both situation which means that at each point, a tangent
can be drawn which in turn gives that the function is differentiable in the interval (a, b).
5. In both situation as the wires at A and B are of equal lengths, i.e., AC = BD, so f (a) = f (b).

6. In view of steps (3), (4) and (5), conditions of Rolle’s theorem are satisfied.
7. From both Fig. we observe that tangents at P as well as Q are parallel to x-axis, therefore f ′(c) at P and also
at Q are zero.

Thus, there exists at least one value c of x in (a, b) such that f ′(c) = 0.
Hence, the Rolle’s theorem is verified.

44