Page 50 - Mathematics Class - XII

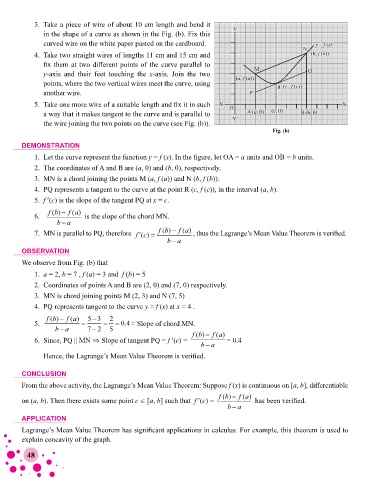
3. Take a piece of wire of about 10 cm length and bend it
in the shape of a curve as shown in the Fig. (b). Fix this
curved wire on the white paper pasted on the cardboard.
4. Take two straight wires of lengths 11 cm and 15 cm and
fix them at two different points of the curve parallel to
y-axis and their feet touching the x-axis. Join the two
points, where the two vertical wires meet the curve, using
another wire.
5. Take one more wire of a suitable length and fix it in such
a way that it makes tangent to the curve and is parallel to
the wire joining the two points on the curve (see Fig. (b)).
Fig. (b)

DEMONSTRATION
1. Let the curve represent the function y = f (x). In the figure, let OA = a units and OB = b units.

2. The coordinates of A and B are (a, 0) and (b, 0), respectively.
3. MN is a chord joining the points M (a, f (a)) and N (b, f (b)).
4. PQ represents a tangent to the curve at the point R (c, f (c)), in the interval (a, b).
5. f ′(c) is the slope of the tangent PQ at x = c.

6. fb() − fa() is the slope of the chord MN.
ba−
7. MN is parallel to PQ, therefore fc() fb () fa() , thus the Lagrange’s Mean Value Theorem is verified.

ba
OBSERVATION
We observe from Fig. (b) that

1. a = 2, b = 7 , f (a) = 3 and f (b) = 5
2. Coordinates of points A and B are (2, 0) and (7, 0) respectively.
3. MN is chord joining points M (2, 3) and N (7, 5)
4. PQ represents tangent to the curve y = f (x) at x = 4 .

fb() fa() 53 2
5. . 04 = Slope of chord MN.
ba 72 5

6. Since, PQ || MN ⇒ Slope of tangent PQ = f ′(c) = fb() − fa() = 0.4
ba−
Hence, the Lagrange’s Mean Value Theorem is verified.

CONCLUSION
From the above activity, the Lagrange’s Mean Value Theorem: Suppose f (x) is continuous on [a, b], differentiable

fb() − fa()
on (a, b). Then there exists some point c ∈ [a, b] such that f ′(c) = has been verified.
ba−
APPLICATION

Lagrange’s Mean Value Theorem has significant applications in calculus. For example, this theorem is used to
explain concavity of the graph.

48