Page 42 - Mathematics Class - XII

ACTIVITY 3.4

OBJECTIVE

To verify that for a function f to be continuous at given point x , Δ y = | f (x + Δ x) – f (x ) | is arbitrarily small
0
0
0
provided Δ x is sufficiently small.
MATERIAL REQUIRED

Y Cardboard Y Scale
Y Graph paper Y Calculator
Y Pencil Y Adhesive

PRE-REQUISITE KNOWLEDGE
1. Knowledge of the concept of the continuity of a function.

PROCEDURE
1. Take cardboard and paste a graph paper on it.

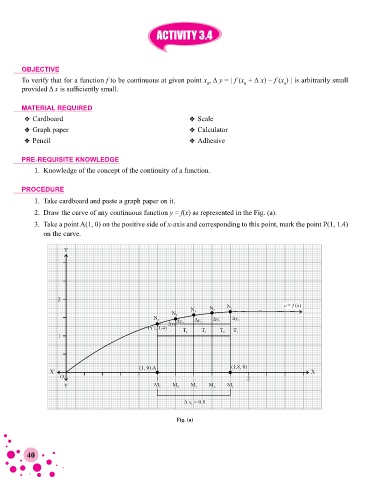
2. Draw the curve of any continuous function y = f(x) as represented in the Fig. (a).
3. Take a point A(1, 0) on the positive side of x-axis and corresponding to this point, mark the point P(1, 1.4)
on the curve.

Y Y

2 2
y y =( )fx=( )fx
N 1 N 1
N 2 N 2
N 3 N 3
N 4 N 4
N 5 N 5 y y
y 11
y 22
y 33
y y
y 44
y
y 55
P(1, 1.4)
P(1, 1.4)
T 4 T 4 T 3 T 3 T 2 T 2 T 1 T 1
1 1
(1.8, 0)
(1, 0) AA
(1, 0) (1.8, 0)
X´
X´ X X
O O 1 1 2 2
Y´
Y´ M M M M M
M 55
M 44
M 33
M 11
M 22
= 0.8
x 1 = 0.8x 1
Fig. (a)
40