Page 97 - Mathematics Class - IX

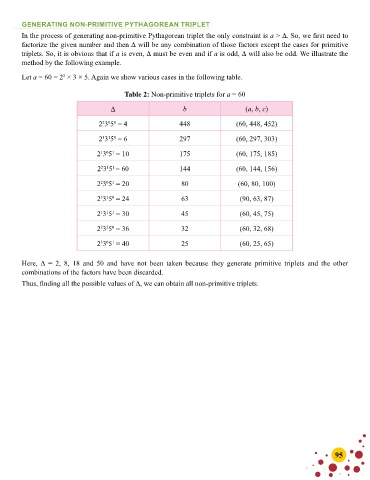
GENERATING NON-PRIMITIVE PYTHAGOREAN TRIPLET
In the process of generating non-primitive Pythagorean triplet the only constraint is a > ∆. So, we first need to
factorize the given number and then ∆ will be any combination of those factors except the cases for primitive
triplets. So, it is obvious that if a is even, ∆ must be even and if a is odd, ∆ will also be odd. We illustrate the
method by the following example.

Let a = 60 = 2 × 3 × 5. Again we show various cases in the following table.
2
Table 2: Non-primitive triplets for a = 60

∆ b (a, b, c)
2 3 5 = 4 448 (60, 448, 452)
2 0 0

2 3 5 = 6 297 (60, 297, 303)
1 1 0
2 3 5 = 10 175 (60, 175, 185)
1 0 1
2 3 5 = 60 144 (60, 144, 156)
2 1 1
2 3 5 = 20 80 (60, 80, 100)
2 0 1
2 3 5 = 24 63 (90, 63, 87)
3 1 0
2 3 5 = 30 45 (60, 45, 75)
1 1 1
2 3 5 = 36 32 (60, 32, 68)
2 2 0
2 3 5 = 40 25 (60, 25, 65)
3 0 1

Here, ∆ = 2, 8, 18 and 50 and have not been taken because they generate primitive triplets and the other
combinations of the factors have been discarded.

Thus, finding all the possible values of ∆, we can obtain all non-primitive triplets.

95