Page 16 - Mathematics Class - XI

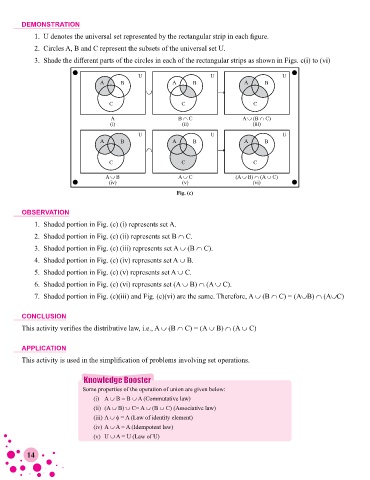
DEMONSTRATION
1. U denotes the universal set represented by the rectangular strip in each figure.

2. Circles A, B and C represent the subsets of the universal set U.
3. Shade the different parts of the circles in each of the rectangular strips as shown in Figs. c(i) to (vi)

U U U
A B A B A B
∪ →

C C C

A B ∩ C A ∪ (B ∩ C)
(i) (ii) (iii)
U U U
A B A B A B
∩ →

C C C

A ∪ B A ∪ C (A ∪ B) ∩ (A ∪ C)
(iv) (v) (vi)
Fig. (c)

OBSERVATION
1. Shaded portion in Fig. (c) (i) represents set A.

2. Shaded portion in Fig. (c) (ii) represents set B ∩ C.
3. Shaded portion in Fig. (c) (iii) represents set A ∪ (B ∩ C).

4. Shaded portion in Fig. (c) (iv) represents set A ∪ B.
5. Shaded portion in Fig. (c) (v) represents set A ∪ C.

6. Shaded portion in Fig. (c) (vi) represents set (A ∪ B) ∩ (A ∪ C).
7. Shaded portion in Fig. (c)(iii) and Fig. (c)(vi) are the same. Therefore, A ∪ (B ∩ C) = (A∪B) ∩ (A∪C)

CONCLUSION

This activity verifies the distributive law, i.e., A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)

APPLICATION
This activity is used in the simplification of problems involving set operations.

Knowledge Booster
Some properties of the operation of union are given below:
(i) A ∪ B = B ∪ A (Commutative law)
(ii) (A ∪ B) ∪ C= A ∪ (B ∪ C) (Associative law)
(iii) A ∪ φ = A (Law of identity element)
(iv) A ∪ A = A (Idempotent law)
(v) U ∪ A = U (Law of U)

14