Page 13 - Mathematics Class - XI

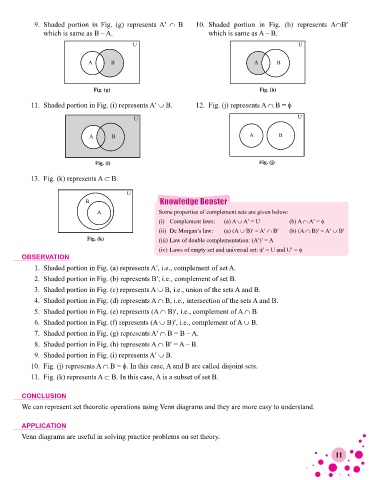
9. Shaded portion in Fig. (g) represents A′ ∩ B 10. Shaded portion in Fig. (h) represents A∩B′
which is same as B – A. which is same as A – B.
U U

A B A B

Fig. (g) Fig. (h)

11. Shaded portion in Fig. (i) represents A′ ∪ B. 12. Fig. (j) represents A ∩ B = φ

U U

A B A B

Fig. (i) Fig. (j)

13. Fig. (k) represents A ⊂ B.

U
B Knowledge Booster
A Some properties of complement sets are given below:
(i) Complement laws: (a) A ∪ A′ = U (b) A ∩ A′ = φ
(ii) De Morgan’s law: (a) (A ∪ B)′ = A′ ∩ B′ (b) (A ∩ B)′ = A′ ∪ B′
Fig. (k) (iii) Law of double complementation: (A′)′ = A

(iv) Laws of empty set and universal set: φ′ = U and U′ = φ
OBSERVATION
1. Shaded portion in Fig. (a) represents A′, i.e., complement of set A.
2. Shaded portion in Fig. (b) represents B′, i.e., complement of set B.

3. Shaded portion in Fig. (c) represents A ∪ B, i.e., union of the sets A and B.
4. Shaded portion in Fig. (d) represents A ∩ B, i.e., intersection of the sets A and B.
5. Shaded portion in Fig. (e) represents (A ∩ B)′, i.e., complement of A ∩ B.
6. Shaded portion in Fig. (f) represents (A ∪ B)′, i.e., complement of A ∪ B.

7. Shaded portion in Fig. (g) represents A′ ∩ B = B – A.
8. Shaded portion in Fig. (h) represents A ∩ B′ = A – B.
9. Shaded portion in Fig. (i) represents A′ ∪ B.
10. Fig. (j) represents A ∩ B = φ. In this case, A and B are called disjoint sets.

11. Fig. (k) represents A ⊂ B. In this case, A is a subset of set B.

CONCLUSION
We can represent set theoretic operations using Venn diagrams and they are more easy to understand.

APPLICATION
Venn diagrams are useful in solving practice problems on set theory.

11