Page 97 - Maths Skills - 8

Factorisation 95

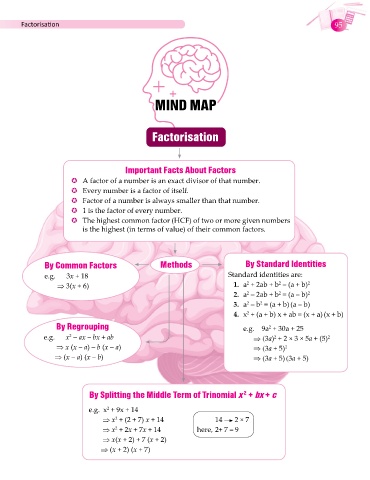
MIND MAP

Factorisation

Important Facts About Factors
� A factor of a number is an exact divisor of that number.
� Every number is a factor of itself.
� Factor of a number is always smaller than that number.

� 1 is the factor of every number.
� The highest common factor (HCF) of two or more given numbers
is the highest (in terms of value) of their common factors.

By Common Factors Methods By Standard Identities
e.g. 3x + 18 Standard identities are:
2
2
⇒ 3(x + 6) 1. a + 2ab + b = (a + b) 2
2. a – 2ab + b = (a – b) 2
2
2
3. a – b = (a + b)(a – b)
2

2
4. x + (a + b) x + ab = (x + a)(x + b)
2

By Regrouping e.g. 9a + 30a + 25
2
e.g. x – ax – bx + ab ⇒ (3a) + 2 × 3 × 5a + (5) 2
2
2
⇒ x (x – a) – b (x – a) ⇒ (3a + 5) 2
⇒ (x – a) (x – b) ⇒ (3a + 5)(3a + 5)

By Splitting the Middle Term of Trinomial x + bx + c
2
e.g. x + 9x + 14
2
⇒ x + (2 + 7) x + 14 14 2 × 7
2
⇒ x + 2x + 7x + 14 here, 2+ 7 = 9
2
⇒ x(x + 2) + 7 (x + 2)
⇒ (x + 2) (x + 7)