Page 30 - Maths Skills - 8

28 Maths

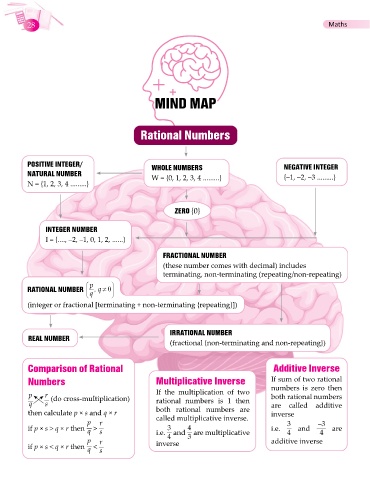
MIND MAP

Rational Numbers

POSITIVE INTEGER/ WHOLE NUMBERS NEGATIVE INTEGER
NATURAL NUMBER W = {0, 1, 2, 3, 4 .........} {–1, –2, –3 .........}
N = {1, 2, 3, 4 .........}

ZERO {0}

INTEGER NUMBER
I = {...., –2, –1, 0, 1, 2, ......}

FRACTIONAL NUMBER
(these number comes with decimal) includes
terminating, non-terminating (repeating/non-repeating)
p
RATIONAL NUMBER q q , 0

(integer or fractional [terminating + non-terminating {repeating}])

IRRATIONAL NUMBER
REAL NUMBER
(fractional {non-terminating and non-repeating})

Comparison of Rational Additive Inverse
Numbers Multiplicative Inverse If sum of two rational
numbers is zero then
p r (do cross-multiplication) If the multiplication of two both rational numbers
q s rational numbers is 1 then are called additive
then calculate p × s and q × r both rational numbers are inverse
p r called multiplicative inverse. 3 –3
3
4
if p × s > q × r then > s i.e. and are multiplicative i.e. 4 and 4 are
q
p r 4 3 additive inverse
if p × s < q × r then < s inverse
q