Page 32 - Mathematics Class - XII

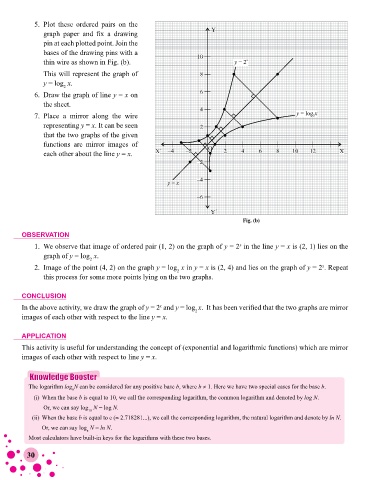
5. Plot these ordered pairs on the
graph paper and fix a drawing Y Y
pin at each plotted point. Join the
bases of the drawing pins with a
thin wire as shown in Fig. (b). 10 10 y = 2= 2 x x
y
This will represent the graph of 8 8
y = log x.
2
6. Draw the graph of line y = x on 6 6
the sheet.
4 4
7. Place a mirror along the wire y x
y = log 2 x= log 2
representing y = x. It can be seen 2 2
that the two graphs of the given
functions are mirror images of
each other about the line y = x. X´ –4 –4 –2 –2 O O 2 2 4 4 6 6 8 8 10 10 12 X X
12
X´
–2 –2

–4
–4
y = x= x
y
–6
–6
Y´
Y´
Fig. (b)

OBSERVATION
1. We observe that image of ordered pair (1, 2) on the graph of y = 2 in the line y = x is (2, 1) lies on the
x
graph of y = log x.
2
2. Image of the point (4, 2) on the graph y = log x in y = x is (2, 4) and lies on the graph of y = 2 . Repeat
x
2
this process for some more points lying on the two graphs.

CONCLUSION
In the above activity, we draw the graph of y = 2 and y = log x. It has been verified that the two graphs are mirror
x
2
images of each other with respect to the line y = x.

APPLICATION

This activity is useful for understanding the concept of (exponential and logarithmic functions) which are mirror
images of each other with respect to line y = x.

Knowledge Booster

The logarithm log N can be considered for any positive base b, where b ≠ 1. Here we have two special cases for the base b.
b
(i) When the base b is equal to 10, we call the corresponding logarithm, the common logarithm and denoted by log N.
Or, we can say log N = log N.
10
(ii) When the base b is equal to e (≈ 2.718281...), we call the corresponding logarithm, the natural logarithm and denote by ln N.
Or, we can say log N = ln N.
e
Most calculators have built-in keys for the logarithms with these two bases.

30