Page 60 - Mathematics Class - X

ACTIVITY 4.4

OBJECTIVE
To verify Pythagoras theorem.

MATERIALS REQUIRED

White sheets of paper A pair of scissors
Geometry box with pencil Adhesive fevicol/glue etc.
Coloured glaze papers of different colours

PRE-REQUISITE KNOWLEDGE
1. Concept of a trapezium and a right angled triangle.
2. The identity (a + b) = a + b + 2ab
2
2
2

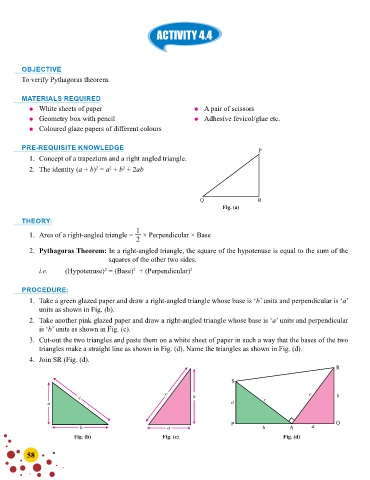
Fig. (a)

THEORY:
1
1. Area of a right-angled triangle = × Perpendicular × Base
2

2. Pythagoras Theorem: In a right-angled triangle, the square of the hypotenuse is equal to the sum of the
squares of the other two sides.

i.e. (Hypotenuse) = (Base) + (Perpendicular) 2
2
2
PROCEDURE:
1. Take a green glazed paper and draw a right-angled triangle whose base is ‘b’ units and perpendicular is ‘a’
units as shown in Fig. (b).
2. Take another pink glazed paper and draw a right-angled triangle whose base is ‘a’ units and perpendicular
is ‘b’ units as shown in Fig. (c).
3. Cut-out the two triangles and paste them on a white sheet of paper in such a way that the bases of the two
triangles make a straight line as shown in Fig. (d). Name the triangles as shown in Fig. (d).
4. Join SR (Fig. (d).

Fig. (b) Fig. (c) Fig. (d)

58