Page 20 - Mathematics Class - X

Y

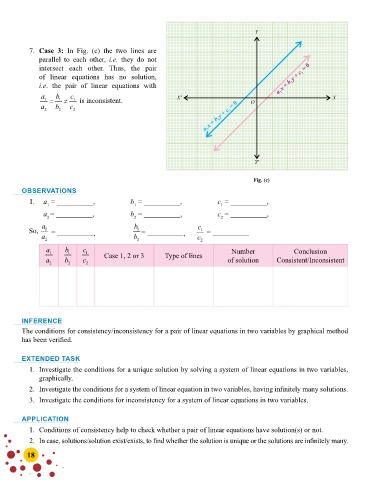
7. Case 3: In Fig. (c) the two lines are
parallel to each other, i.e. they do not
intersect each other. Thus, the pair
of linear equations has no solution,
i.e. the pair of linear equations with
a 1 = b 1 ≠ c 1 is inconsistent. X′ X
a 2 b 2 c 2 O

Y′

Fig. (c)
OBSERVATIONS
1. a = __________, b = __________, c = __________,
1
1
1
a = __________, b = __________, c = __________,
2 2 2
a b c
So, 1 = __________ , 1 = __________ , 1 = __________
a 2 b 2 c 2
a 1 b 1 c 1 Number Conclusion

a 2 b 2 c 2 Case 1, 2 or 3 Type of lines of solution Consistent/Inconsistent

INFERENCE
The conditions for consistency/inconsistency for a pair of linear equations in two variables by graphical method
has been verified.

EXTENDED TASK
1. Investigate the conditions for a unique solution by solving a system of linear equations in two variables,
graphically.
2. Investigate the conditions for a system of linear equation in two variables, having infinitely many solutions.

3. Investigate the conditions for inconsistency for a system of linear equations in two variables.

APPLICATION
1. Conditions of consistency help to check whether a pair of linear equations have solution(s) or not.
2. In case, solutions/solution exist/exists, to find whether the solution is unique or the solutions are infinitely many.

18