Page 19 - Mathematics Class - X

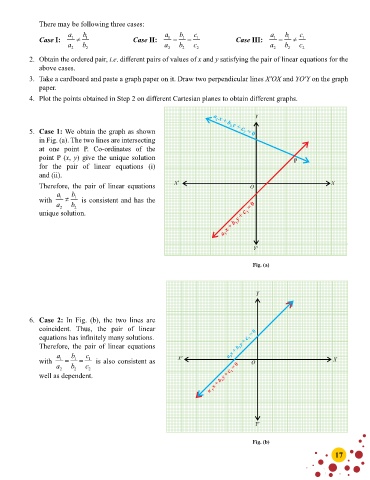
There may be following three cases:
a b a b c a b c
Case I: 1 ≠ 1 Case II: 1 = 1 = 1 Case III: 1 = 1 ≠ 1
a 2 b 2 a 2 b 2 c 2 a 2 b 2 c 2
2. Obtain the ordered pair, i.e. different pairs of values of x and y satisfying the pair of linear equations for the
above cases.
3. Take a cardboard and paste a graph paper on it. Draw two perpendicular lines X′OX and YO′Y on the graph
paper.
4. Plot the points obtained in Step 2 on different Cartesian planes to obtain different graphs.

Y

5. Case 1: We obtain the graph as shown
in Fig. (a). The two lines are intersecting
at one point P. Co-ordinates of the
point P (x, y) give the unique solution
for the pair of linear equations (i)
and (ii).
Therefore, the pair of linear equations X′ O X
a b
with 1 ≠ 1 is consistent and has the
a 2 b 2
unique solution.

Y′

Fig. (a)

Y

6. Case 2: In Fig. (b), the two lines are
coincident. Thus, the pair of linear
equations has infinitely many solutions.
Therefore, the pair of linear equations
a b c X′
with 1 = 1 = 1 is also consistent as O X
a 2 b 2 c 2
well as dependent.

Y′

Fig. (b)

17