Page 23 - Mathematics Class - X
P. 23
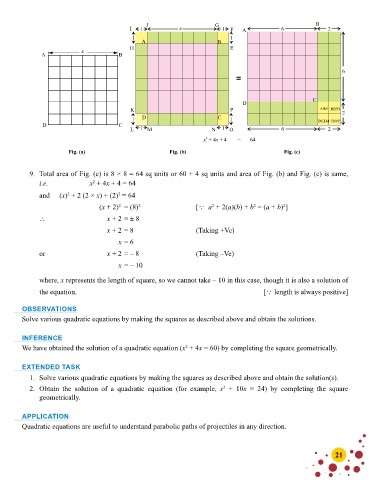
J G B
I F A
A B
H E
x
A B
C
D
K P AHIJ BEFG
D C
D C L M N O DKLM CNOP
Fig. (a) Fig. (b) Fig. (c)
9. Total area of Fig. (c) is 8 × 8 = 64 sq units or 60 + 4 sq units and area of Fig. (b) and Fig. (c) is same,
i.e. x + 4x + 4 = 64
2
and (x) + 2 (2 × x) + (2) = 64
2
2
(x + 2) = (8) 2 [Q a + 2(a)(b) + b = (a + b) ]
2
2
2
2
\ x + 2 = ± 8
x + 2 = 8 (Taking +Ve)
x = 6
or x + 2 = – 8 (Taking –Ve)
x = – 10
where, x represents the length of square, so we cannot take – 10 in this case, though it is also a solution of
the equation. [Q length is always positive]
OBSERVATIONS
Solve various quadratic equations by making the squares as described above and obtain the solutions.
INFERENCE
We have obtained the solution of a quadratic equation (x + 4x = 60) by completing the square geometrically.
2
EXTENDED TASK
1. Solve various quadratic equations by making the squares as described above and obtain the solution(s).
2. Obtain the solution of a quadratic equation (for example, x + 10x = 24) by completing the square
2
geometrically.
APPLICATION
Quadratic equations are useful to understand parabolic paths of projectiles in any direction.
21