Page 86 - Maths Skills - 8

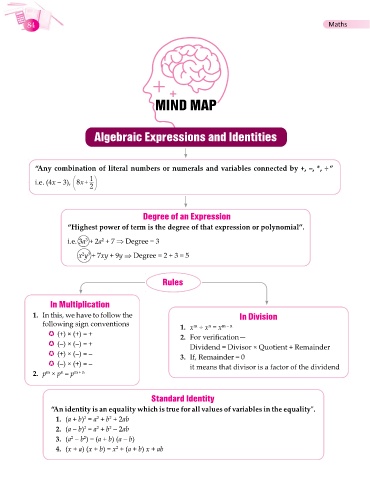
84 Maths

MIND MAP

Algebraic Expressions and Identities

“Any combination of literal numbers or numerals and variables connected by +, –, *, ÷ ”

x
i.e. (4x – 3), 8+ 1

2

Degree of an Expression
“Highest power of term is the degree of that expression or polynomial”.

i.e. 3a + 2a + 7 ⇒ Degree = 3
2
3
x y + 7xy + 9y ⇒ Degree = 2 + 3 = 5
2 3

Rules

In Multiplication
1. In this, we have to follow the In Division
following sign conventions 1. x ÷ x = x m – n
m
n
� (+) × (+) = + 2. For verification—
� (–) × (–) = + Dividend = Divisor × Quotient + Remainder
� (+) × (–) = – 3. If, Remainder = 0
� (–) × (+) = – it means that divisor is a factor of the dividend
2. p × p = p m + n
m
n

Standard Identity
“An identity is an equality which is true for all values of variables in the equality".
1. (a + b) = a + b + 2ab
2
2
2
2. (a – b) = a + b – 2ab
2
2
2
3. (a – b ) = (a + b) (a – b)
2
2
4. (x + a) (x + b) = x + (a + b) x + ab
2