Page 85 - Maths Skills - 8

Algebraic Expressions and Identities 83

2. Simplify the following:

(i) (a + b + c) + (a – b – c) (ii) (a – b + c) – (a – b – c) 2
2
2
2
(iii) (–2x – 3y + 5z) – (2x + 3y – 5z) (iv) (l + 2m – 3n) – (l – 2m + 3n) 2
2
2
2
Word Stock
Degree Algebra Variable Identity Polynomial Constant Literal

Activity

Objective: To verify the following algebraic identity experimentally.
(x + a) (x + b) = x + ax + bx + ab = x + (a + b)x + ab
2
2
Pre-Requisite Knowledge: 1. Concept of monomials and binomials.
2. Concept of area of a square and a rectangle.
Materials Required: Four different coloured papers, a pair of scissors, a pencil, an eraser, sketch pens, construction
box and fevicol.
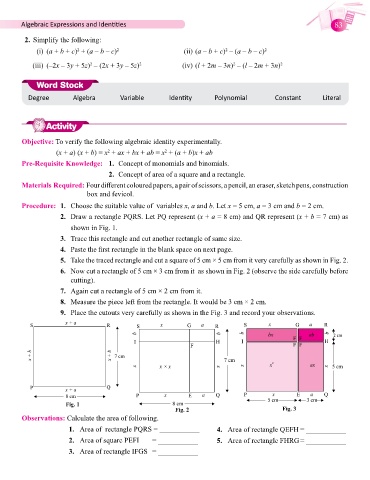
Procedure: 1. Choose the suitable value of variables x, a and b. Let x = 5 cm, a = 3 cm and b = 2 cm.

2. Draw a rectangle PQRS. Let PQ represent (x + a = 8 cm) and QR represent (x + b = 7 cm) as
shown in Fig. 1.
3. Trace this rectangle and cut another rectangle of same size.
4. Paste the first rectangle in the blank space on next page.

5. Take the traced rectangle and cut a square of 5 cm × 5 cm from it very carefully as shown in Fig. 2.
6. Now cut a rectangle of 5 cm × 3 cm from it as shown in Fig. 2 (observe the side carefully before
cutting).
7. Again cut a rectangle of 5 cm × 2 cm from it.
8. Measure the piece left from the rectangle. It would be 3 cm × 2 cm.
9. Place the cutouts very carefully as shown in the Fig. 3 and record your observations.

Fig. 1
Fig. 2 Fig. 3
Observations: Calculate the area of following.
1. Area of rectangle PQRS = ___________ 4. Area of rectangle QEFH = ___________

2. Area of square PEFI = ___________ 5. Area of rectangle FHRG = ___________

3. Area of rectangle IFGS = ___________