Page 167 - Maths Skills - 8

Understanding Quadrilaterals 165

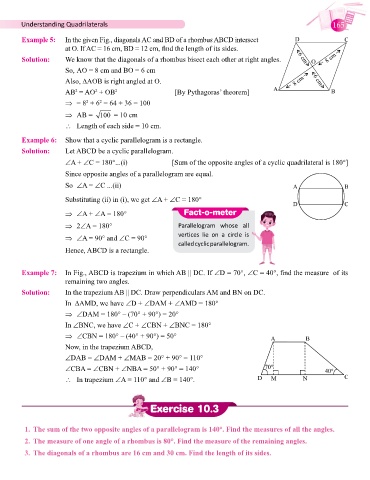
Example 5: In the given Fig., diagonals AC and BD of a rhombus ABCD intersect
at O. If AC = 16 cm, BD = 12 cm, find the length of its sides.
Solution: We know that the diagonals of a rhombus bisect each other at right angles.
So, AO = 8 cm and BO = 6 cm

Also, DAOB is right angled at O.
AB = AO + OB [By Pythagoras’ theorem]
2
2
2
⇒ = 8 + 6 = 64 + 36 = 100
2
2
⇒ AB = 100 = 10 cm
∴ Length of each side = 10 cm.
Example 6: Show that a cyclic parallelogram is a rectangle.
Solution: Let ABCD be a cyclic parallelogram.
∠A + ∠C = 180°...(i) [Sum of the opposite angles of a cyclic quadrilateral is 180°]

Since opposite angles of a parallelogram are equal.
So ∠A = ∠C ...(ii)

Substituting (ii) in (i), we get ∠A + ∠C = 180°

⇒ ∠A + ∠A = 180° Fact-o-meter

⇒ 2∠A = 180° Parallelogram whose all
⇒ ∠A = 90° and ∠C = 90° vertices lie on a circle is
called cyclic parallelogram.
Hence, ABCD is a rectangle.

Example 7: In Fig., ABCD is trapezium in which AB || DC. If ∠D = 70°, ∠C = 40°, find the measure of its
remaining two angles.
Solution: In the trapezium AB || DC. Draw perpendiculars AM and BN on DC.

In DAMD, we have ∠D + ∠DAM + ∠AMD = 180°
⇒ ∠DAM = 180° – (70° + 90°) = 20°
In ∠BNC, we have ∠C + ∠CBN + ∠BNC = 180°
⇒ ∠CBN = 180° – (40° + 90°) = 50°
Now, in the trapezium ABCD,

∠DAB = ∠DAM + ∠MAB = 20° + 90° = 110°
∠CBA = ∠CBN + ∠NBA = 50° + 90° = 140°
∴ In trapezium ∠A = 110° and ∠B = 140°.

Exercise 10.3

1. The sum of the two opposite angles of a parallelogram is 140°. Find the measures of all the angles.
2. The measure of one angle of a rhombus is 80°. Find the measure of the remaining angles.
3. The diagonals of a rhombus are 16 cm and 30 cm. Find the length of its sides.