Page 191 - Maths Skills - 7

Symmetry 189

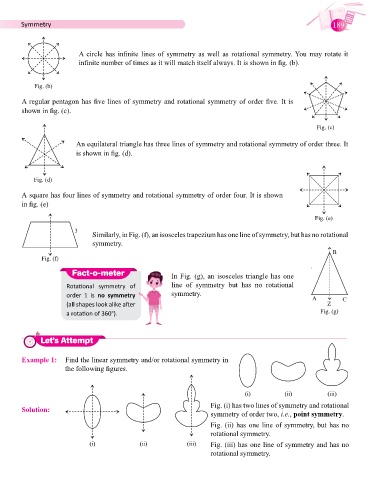
A circle has infinite lines of symmetry as well as rotational symmetry. You may rotate it
infinite number of times as it will match itself always. It is shown in fig. (b).

Fig. (b)

A regular pentagon has five lines of symmetry and rotational symmetry of order five. It is
shown in fig. (c).

Fig. (c)

An equilateral triangle has three lines of symmetry and rotational symmetry of order three. It
is shown in fig. (d).

Fig. (d)

A square has four lines of symmetry and rotational symmetry of order four. It is shown
in fig. (e)

Fig. (e)

3
Similarly, in Fig. (f), an isosceles trapezium has one line of symmetry, but has no rotational
symmetry.
B
Fig. (f)

Fact-o-meter In Fig. (g), an isosceles triangle has one

Rotational symmetry of line of symmetry but has no rotational
order 1 is no symmetry symmetry. A C
(all shapes look alike after Z
a rotation of 360°). Fig. (g)

Let’s Attempt

Example 1: Find the linear symmetry and/or rotational symmetry in
the following figures.

Solution: Fig. (i) has two lines of symmetry and rotational
symmetry of order two, i.e., point symmetry.

Fig. (ii) has one line of symmetry, but has no
rotational symmetry.

Fig. (iii) has one line of symmetry and has no
rotational symmetry.