Page 46 - Mathematics Class - XI

(ii) For point D (1, 2),
Value of LHS = 5(1) + 4(2) – 40 = –27 < 0
(iii) For point E (3, 2),

Value of LHS = 5(3) + 4(2) – 40 = –17 < 0
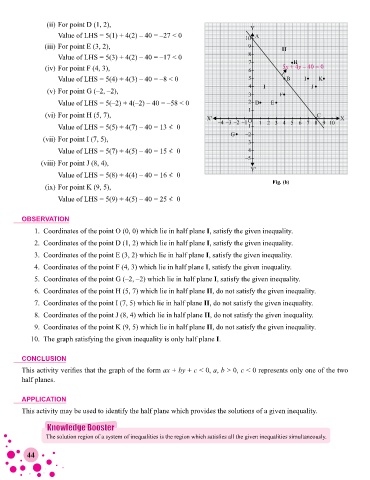
(iv) For point F (4, 3), 5x + 4y – 40 = 0
Value of LHS = 5(4) + 4(3) – 40 = –8 < 0

(v) For point G (–2, –2),
Value of LHS = 5(–2) + 4(–2) – 40 = –58 < 0

(vi) For point H (5, 7),
Value of LHS = 5(5) + 4(7) – 40 = 13 </ 0

(vii) For point I (7, 5),
Value of LHS = 5(7) + 4(5) – 40 = 15 </ 0
(viii) For point J (8, 4),

Value of LHS = 5(8) + 4(4) – 40 = 16 </ 0
Fig. (b)
(ix) For point K (9, 5),
Value of LHS = 5(9) + 4(5) – 40 = 25 </ 0

OBSERVATION
1. Coordinates of the point O (0, 0) which lie in half plane I, satisfy the given inequality.

2. Coordinates of the point D (1, 2) which lie in half plane I, satisfy the given inequality.

3. Coordinates of the point E (3, 2) which lie in half plane I, satisfy the given inequality.
4. Coordinates of the point F (4, 3) which lie in half plane I, satisfy the given inequality.
5. Coordinates of the point G (–2, –2) which lie in half plane I, satisfy the given inequality.

6. Coordinates of the point H (5, 7) which lie in half plane II, do not satisfy the given inequality.
7. Coordinates of the point I (7, 5) which lie in half plane II, do not satisfy the given inequality.

8. Coordinates of the point J (8, 4) which lie in half plane II, do not satisfy the given inequality.
9. Coordinates of the point K (9, 5) which lie in half plane II, do not satisfy the given inequality.

10. The graph satisfying the given inequality is only half plane I.

CONCLUSION
This activity verifies that the graph of the form ax + by + c < 0, a, b > 0, c < 0 represents only one of the two
half planes.

APPLICATION

This activity may be used to identify the half plane which provides the solutions of a given inequality.

Knowledge Booster
The solution region of a system of inequalities is the region which satisfies all the given inequalities simultaneously.

44