Page 146 - Maths Skills - 8
P. 146
144 Maths
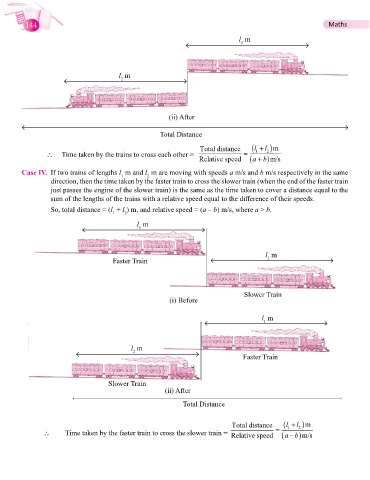
l m
1
l m
2
(ii) After
Total Distance
Total distance (l + l m )
\ Time taken by the trains to cross each other = = 1 2
+ )
Relative speed (ab m/s
Case IV. If two trains of lengths l m and l m are moving with speeds a m/s and b m/s respectively in the same
1
2
direction, then the time taken by the faster train to cross the slower train (when the end of the faster train
just passes the engine of the slower train) is the same as the time taken to cover a distance equal to the
sum of the lengths of the trains with a relative speed equal to the difference of their speeds.
So, total distance = (l + l ) m, and relative speed = (a – b) m/s, where a > b.
1
2
l m
1
l m
Faster Train 2
Slower Train
(i) Before
l m
1
l m
2
Faster Train
Slower Train
(ii) After
Total Distance
Total distance l 1 l 2 m
\ Time taken by the faster train to cross the slower train = Relative speed ab m/s