Page 145 - Maths Skills - 8

Direct and Inverse Proportions 143

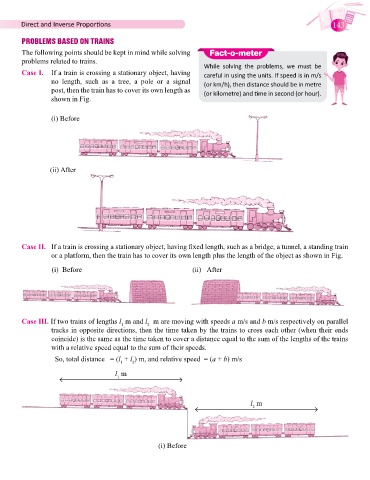
PROBLEMS BASED ON TRAINS
The following points should be kept in mind while solving Fact-o-meter
problems related to trains.
Case I. If a train is crossing a stationary object, having While solving the problems, we must be
careful in using the units. If speed is in m/s
no length, such as a tree, a pole or a signal (or km/h), then distance should be in metre
post, then the train has to cover its own length as (or kilometre) and time in second (or hour).
shown in Fig.

(i) Before

(ii) After

Case II. If a train is crossing a stationary object, having fixed length, such as a bridge, a tunnel, a standing train
or a platform, then the train has to cover its own length plus the length of the object as shown in Fig.
(i) Before (ii) After

Case III. If two trains of lengths l m and l m are moving with speeds a m/s and b m/s respectively on parallel
2
1
tracks in opposite directions, then the time taken by the trains to cross each other (when their ends
coincide) is the same as the time taken to cover a distance equal to the sum of the lengths of the trains
with a relative speed equal to the sum of their speeds.
So, total distance = (l + l ) m, and relative speed = (a + b) m/s
1 2
l m
1

l m
2

(i) Before