Page 165 - Maths Skills - 7
P. 165
Lines and Angles 163
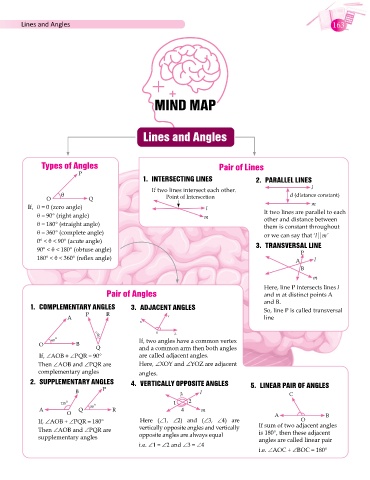
MIND MAP
Lines and Angles
Types of Angles Pair of Lines
P
1. INTERSECTING LINES 2. PARALLEL LINES
If two lines intersect each other. l
θ d (distance constant)
O Q Point of Intersection
If, θ = 0 (zero angle) l m
θ = 90° (right angle) m It two lines are parallel to each
other and distance between
θ = 180° (straight angle) them is constant throughout
θ = 360° (complete angle) or we can say that ‘l || m’
0° < θ < 90° (acute angle)
90° < θ < 180° (obtuse angle) 3. TRANSVERSAL LINE
P
180° < θ < 360° (reflex angle) A l
B
m
Here, line P intersects lines l
Pair of Angles and m at distinct points A
and B.
1. COMPLEMENTARY ANGLES 3. ADJACENT ANGLES So, line P is called transversal
P R
A Y line
X
O
30° Z
60° If, two angles have a common vertex
O B Q and a common arm then both angles
If, ∠AOB + ∠PQR = 90° are called adjacent angles.
Then ∠AOB and ∠PQR are Here, ∠XOY and ∠YOZ are adjacent
complementary angles angles.
2. SUPPLEMENTARY ANGLES 4. VERTICALLY OPPOSITE ANGLES 5. LINEAR PAIR OF ANGLES
B P 3 l C
125° 55° 1 2
A O Q R 4 m A B
O
If, ∠AOB + ∠PQR = 180° Here (∠1, ∠2) and (∠3, ∠4) are If sum of two adjacent angles
Then ∠AOB and ∠PQR are vertically opposite angles and vertically is 180°, then these adjacent
supplementary angles opposite angles are always equal angles are called linear pair
i.e. ∠1 = ∠2 and ∠3 = ∠4
i.e. ∠AOC + ∠BOC = 180°