Page 188 - Math Skill - 5

186 Maths

Patterns in Square Numbers
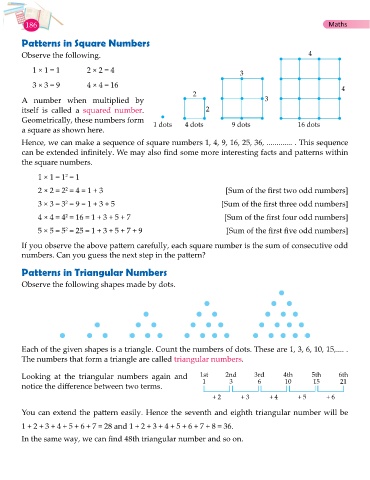
Observe the following. 4

1 × 1 = 1 2 × 2 = 4 3

3 × 3 = 9 4 × 4 = 16 4
2
A number when multiplied by 3
itself is called a squared number. 2
Geometrically, these numbers form 1 dots 4 dots 9 dots 16 dots
a square as shown here.
Hence, we can make a sequence of square numbers 1, 4, 9, 16, 25, 36, ............. . This sequence
can be extended infinitely. We may also find some more interesting facts and patterns within
the square numbers.

1 × 1 = 1 = 1
2
2 × 2 = 2 = 4 = 1 + 3 [Sum of the first two odd numbers]
2
3 × 3 = 3 = 9 = 1 + 3 + 5 [Sum of the first three odd numbers]
2
4 × 4 = 4 = 16 = 1 + 3 + 5 + 7 [Sum of the first four odd numbers]
2
5 × 5 = 5 = 25 = 1 + 3 + 5 + 7 + 9 [Sum of the first five odd numbers]
2

If you observe the above pattern carefully, each square number is the sum of consecutive odd
numbers. Can you guess the next step in the pattern?

Patterns in Triangular Numbers

Observe the following shapes made by dots.

Each of the given shapes is a triangle. Count the numbers of dots. These are 1, 3, 6, 10, 15,.... .
The numbers that form a triangle are called triangular numbers.

Looking at the triangular numbers again and 1st 2nd 3rd 4th 5th 6th
notice the difference between two terms. 1 3 6 10 15 21

+ 2 + 3 + 4 + 5 + 6

You can extend the pattern easily. Hence the seventh and eighth triangular number will be

1 + 2 + 3 + 4 + 5 + 6 + 7 = 28 and 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 = 36.
In the same way, we can find 48th triangular number and so on.