Page 79 - Mathematics Class - IX

3. Take string and wrap the ball (spirally) with string completely, by taking support of pin (Fig. (b)).
4. Mark the starting and ending points on the string, (for accuracy, it should be thinner) and measure the length
between these two marks. Mark this as l.
5. Now, unwind the string from the ball.

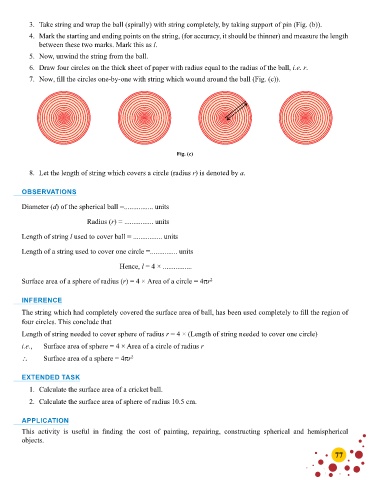
6. Draw four circles on the thick sheet of paper with radius equal to the radius of the ball, i.e. r.
7. Now, fill the circles one-by-one with string which wound around the ball (Fig. (c)).

Fig. (c)

8. Let the length of string which covers a circle (radius r) is denoted by a.

OBSERVATIONS

Diameter (d) of the spherical ball =................ units

Radius (r) = ................ units

Length of string l used to cover ball = ................ units

Length of a string used to cover one circle =............... units

Hence, l = 4 × ................

Surface area of a sphere of radius (r) = 4 × Area of a circle = 4pr 2

INFERENCE
The string which had completely covered the surface area of ball, has been used completely to fill the region of
four circles. This conclude that

Length of string needed to cover sphere of radius r = 4 × (Length of string needed to cover one circle)
i.e., Surface area of sphere = 4 × Area of a circle of radius r

\ Surface area of a sphere = 4pr 2

EXTENDED TASK
1. Calculate the surface area of a cricket ball.

2. Calculate the surface area of sphere of radius 10.5 cm.

APPLICATION
This activity is useful in finding the cost of painting, repairing, constructing spherical and hemispherical
objects.

77