Page 69 - Mathematics Class - XI

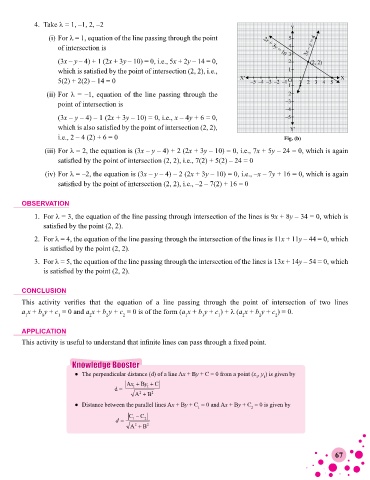
4. Take l = 1, –1, 2, –2

(i) For l = 1, equation of the line passing through the point
of intersection is

(3x – y – 4) + 1 (2x + 3y – 10) = 0, i.e., 5x + 2y – 14 = 0,
which is satisfied by the point of intersection (2, 2), i.e.,
5(2) + 2(2) – 14 = 0
(ii) For l = –1, equation of the line passing through the
point of intersection is

(3x – y – 4) – 1 (2x + 3y – 10) = 0, i.e., x – 4y + 6 = 0,
which is also satisfied by the point of intersection (2, 2),
i.e., 2 – 4 (2) + 6 = 0 Fig. (b)

(iii) For l = 2, the equation is (3x – y – 4) + 2 (2x + 3y – 10) = 0, i.e., 7x + 5y – 24 = 0, which is again
satisfied by the point of intersection (2, 2), i.e., 7(2) + 5(2) – 24 = 0

(iv) For l = –2, the equation is (3x – y – 4) – 2 (2x + 3y – 10) = 0, i.e., –x – 7y + 16 = 0, which is again
satisfied by the point of intersection (2, 2), i.e., –2 – 7(2) + 16 = 0

OBSERVATION

1. For l = 3, the equation of the line passing through intersection of the lines is 9x + 8y – 34 = 0, which is
satisfied by the point (2, 2).
2. For l = 4, the equation of the line passing through the intersection of the lines is 11x + 11y – 44 = 0, which
is satisfied by the point (2, 2).

3. For l = 5, the equation of the line passing through the intersection of the lines is 13x + 14y – 54 = 0, which
is satisfied by the point (2, 2).

CONCLUSION
This activity verifies that the equation of a line passing through the point of intersection of two lines
a x + b y + c = 0 and a x + b y + c = 0 is of the form (a x + b y + c ) + l (a x + b y + c ) = 0.
1 1 1 2 2 2 1 1 1 2 2 2

APPLICATION

This activity is useful to understand that infinite lines can pass through a fixed point.

Knowledge Booster
● The perpendicular distance (d) of a line Ax + By + C = 0 from a point (x , y ) is given by
1 1
Ax + By + C
d = 1 1
A + B 2
2
● Distance between the parallel lines Ax + By + C = 0 and Ax + By + C = 0 is given by
2
1
C − C
d = 1 2
A 2 + B 2

67