Page 86 - Mathematics Class - IX

Here, F= x × f 1 = f
1 x 1

Similarly you can find F , F , F , F
2 3 4 5
x × f f
But F= 6 = 6
6
2x 2
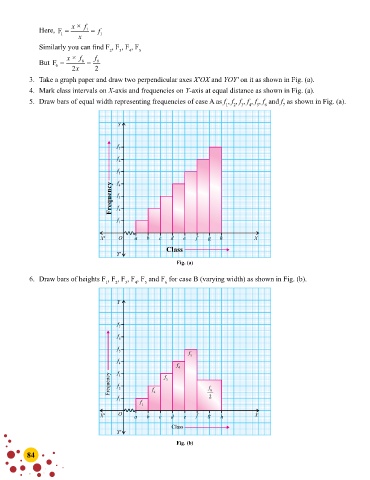
3. Take a graph paper and draw two perpendicular axes X′OX and YOY′ on it as shown in Fig. (a).

4. Mark class intervals on X-axis and frequencies on Y-axis at equal distance as shown in Fig. (a).
5. Draw bars of equal width representing frequencies of case A as f , f , f , f , f , f and f as shown in Fig. (a).
1 2 3 4 5 6 7

Y

f
7
f
6
f
5 4
f
Frequency f f 3

f 2
1

X’ O a b c d e f g h X
Class
Y’
Fig. (a)

6. Draw bars of heights F , F , F , F , F and F for case B (varying width) as shown in Fig. (b).
1 2 3 4 5 6

f 7
f 6

f
5 f
5
f
4 f
4
f 3
f
3
f
2 f f
2 6
f 2
1 f
1
X’
Y’
Fig. (b)

84