Page 28 - Mathematics Class - IX

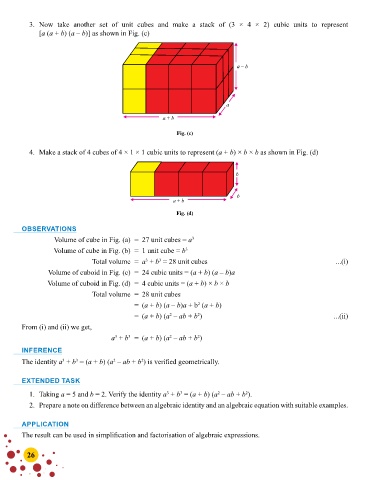
3. Now take another set of unit cubes and make a stack of (3 × 4 × 2) cubic units to represent
[a (a + b) (a – b)] as shown in Fig. (c)

ab–

a

a + b

Fig. (c)

4. Make a stack of 4 cubes of 4 × 1 × 1 cubic units to represent (a + b) × b × b as shown in Fig. (d)

b

b
a + b
Fig. (d)

OBSERVATIONS
Volume of cube in Fig. (a) = 27 unit cubes = a 3

Volume of cube in Fig. (b) = 1 unit cube = b 3
Total volume = a + b = 28 unit cubes ...(i)
3
3
Volume of cuboid in Fig. (c) = 24 cubic units = (a + b) (a – b)a
Volume of cuboid in Fig. (d) = 4 cubic units = (a + b) × b × b

Total volume = 28 unit cubes
= (a + b) (a – b)a + b (a + b)
2
= (a + b) (a – ab + b ) ...(ii)
2
2
From (i) and (ii) we get,
a + b = (a + b) (a – ab + b )
2
2
3
3
INFERENCE
The identity a + b = (a + b) (a – ab + b ) is verified geometrically.
3
3
2
2
EXTENDED TASK
1. Taking a = 5 and b = 2. Verify the identity a + b = (a + b) (a – ab + b ).
2
3
2
3
2. Prepare a note on difference between an algebraic identity and an algebraic equation with suitable examples.
APPLICATION
The result can be used in simplification and factorisation of algebraic expressions.

26