Page 38 - Mathematics Class - X

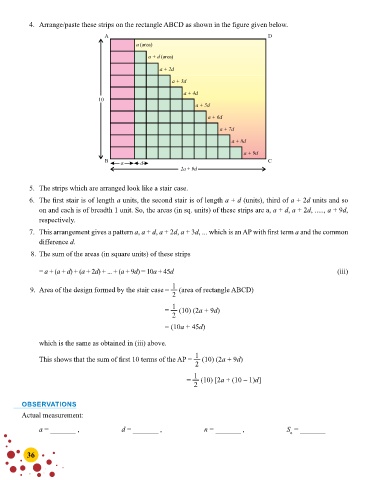
4. Arrange/paste these strips on the rectangle ABCD as shown in the figure given below.

5. The strips which are arranged look like a stair case.
6. The first stair is of length a units, the second stair is of length a + d (units), third of a + 2d units and so
on and each is of breadth 1 unit. So, the areas (in sq. units) of these strips are a, a + d, a + 2d, ....., a + 9d,
respectively.

7. This arrangement gives a pattern a, a + d, a + 2d, a + 3d, ... which is an AP with first term a and the common
difference d.
8. The sum of the areas (in square units) of these strips

= a + (a + d) + (a + 2d) + ... + (a + 9d) = 10a + 45d (iii)

1
9. Area of the design formed by the stair case = (area of rectangle ABCD)
2
1
= (10) (2a + 9d)
2
= (10a + 45d)

which is the same as obtained in (iii) above.
1
This shows that the sum of first 10 terms of the AP = (10) (2a + 9d)
2
1
= (10) [2a + (10 – 1)d]
2

OBSERVATIONS

Actual measurement:

a = _______ , d = _______ , n = _______ , S = _______
n

36